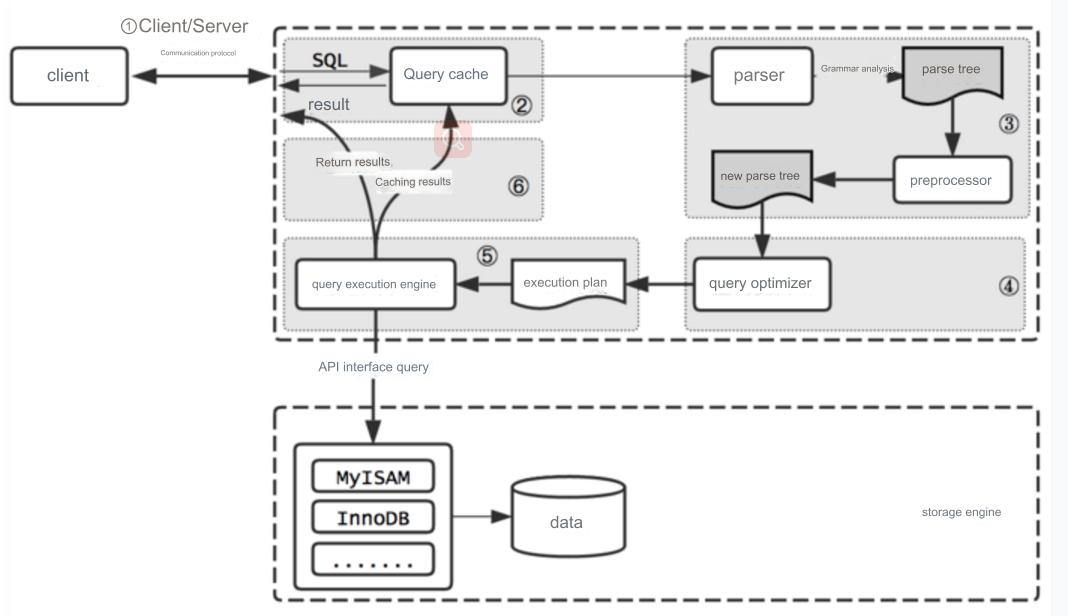
Performance bottlenecks can arise from inefficient database queries, unnecessary recalculations, improper use of data structures, and more. Below, we explore two examples: optimizing a database query and improving algorithm efficiency.

Example 1: Optimizing Database Queries

Suppose we have an e-commerce website storing a large volume of order data, and we want to retrieve all orders for a specific user. Here's an inefficient query:

SELECT * FROM Orders WHERE CustomerID = 12345;

If the Orders table contains millions of records, this query can be slow, especially if the CustomerID field is not indexed. A solution is to index the CustomerID field to allow faster lookups:

CREATE INDEX idx_customer_id ON Orders (CustomerID);

This index significantly improves query performance by enabling the database to quickly locate rows with the desired CustomerID.

Example 2: Optimizing Algorithm and Loops

Consider a Python function to compute the sum of squares for the first n natural numbers:

def sum_of_squares(n):
    total = 0
    for i in range(1, n + 1):
        total += i * i
    return total

This function uses a loop, with a time complexity of $O(n)$. For large $n$, it can become a bottleneck. Using a mathematical formula can eliminate the loop:

def sum_of_squares(n):
    return n * (n + 1) * (2 * n + 1) / 6

This optimized function has a constant time complexity $O(1)$, ensuring fast computation regardless of $n$'s size.

Exploring Advanced Optimization Scenarios

Example 1: Using Advanced Data Structures for Search

Suppose an online bookstore frequently searches for inventory information of books. Using a simple list or array to store book data requires iterating through the list for every search, which is inefficient for large datasets.

Inefficient Approach

books = [
    {"id": 1, "title": "Book A", "inventory": 100},
    {"id": 2, "title": "Book B", "inventory": 50},
    # Thousands of records
]

def search_book_by_title(title):
    for book in books:
        if book["title"] == title:
            return book
    return None

Optimized Approach
Use a hash table (e.g., Python dictionary) to reduce search time from $O(n)$ to $O(1)$:

books_by_title = {
    "Book A": {"id": 1, "inventory": 100},
    "Book B": {"id": 2, "inventory": 50},
    # More books
}

def search_book_by_title(title):
    return books_by_title.get(title, None)

Example 2: Optimizing Complex Database Queries

In a social network application, suppose we want to find user pairs with more than 10 mutual friends. A direct SQL query may require extensive table joins, which are inefficient for large datasets:

Inefficient Query

SELECT a.user_id, b.user_id
FROM friendships a
JOIN friendships b ON a.friend_id = b.friend_id
GROUP BY a.user_id, b.user_id
HAVING COUNT(*) > 10;

Optimized Approach
Use materialized views to pre-compute and store results, avoiding repeated calculations:

CREATE MATERIALIZED VIEW common_friends_count AS
SELECT a.user_id, b.user_id, COUNT(*) AS common_count
FROM friendships a
JOIN friendships b ON a.friend_id = b.friend_id
GROUP BY a.user_id, b.user_id;

SELECT user_id1, user_id2 FROM common_friends_count WHERE common_count > 10;

Materialized views reduce computational overhead during queries by leveraging pre-calculated data.

Example 3: Dynamic Programming for Complex Algorithms

Consider solving the knapsack problem, where we maximize the total value of items in a knapsack without exceeding its weight limit. A recursive solution results in significant repeated calculations:

Inefficient Recursive Solution

def knapsack(W, weights, values, n):
    if n == 0 or W == 0:
        return 0
    if weights[n - 1] > W:
        return knapsack(W, weights, values, n - 1)
    else:
        return max(values[n - 1] + knapsack(W - weights[n - 1], weights, values, n - 1),
                   knapsack(W, weights, values, n - 1))

Optimized Dynamic Programming Solution
Dynamic programming avoids repeated calculations by storing intermediate results:

def knapsack(W, weights, values, n):
    K = [[0 for _ in range(W + 1)] for _ in range(n + 1)]
    for i in range(n + 1):
        for w in range(W + 1):
            if i == 0 or w == 0:
                K[i][w] = 0
            elif weights[i - 1] <= w:
                K[i][w] = max(values[i - 1] + K[i - 1][w - weights[i - 1]], K[i - 1][w])
            else:
                K[i][w] = K[i - 1][w]
    return K[n][W]

This approach reduces the time complexity significantly, ensuring efficient computation even for larger inputs.

Conclusion

These examples demonstrate how to identify and address performance bottlenecks, whether in database queries, data structures, or algorithms. Regular performance evaluations and targeted optimizations ensure that applications run efficiently and respond quickly to user demands.