Quick Sort in Python
Quick Sort is a sorting algorithm that uses the divide and conquer strategy to split a list into smaller and larger sub-lists, and then recursively sort the sub-lists.
The steps are as follows:
Choose a pivot: Select an element from the array as the "pivot."
Partitioning: Reorder the array such that all elements smaller than the pivot are placed before it, and all elements greater than the pivot are placed after it. Elements equal to the pivot can go on either side. After partitioning, the pivot element is in its final position.
Recursively apply the above steps to the sub-lists of smaller and larger elements.
The recursion ends when the sub-lists contain only one or zero elements, which are inherently sorted.
The choice of the pivot is crucial to the performance of the algorithm.
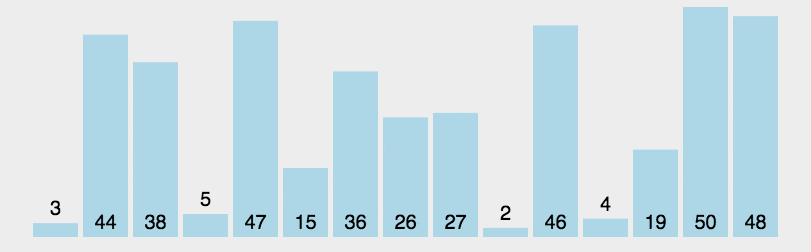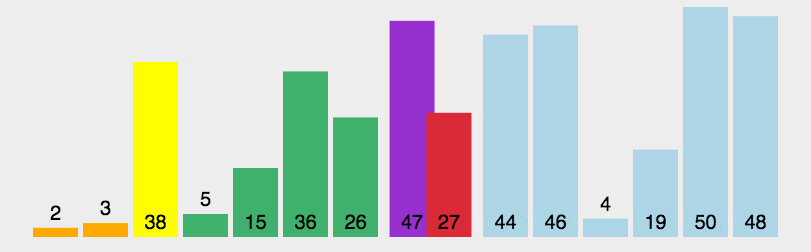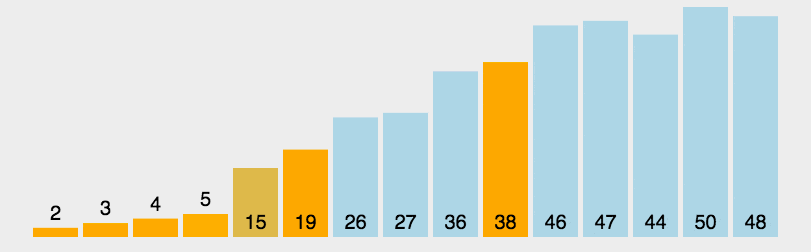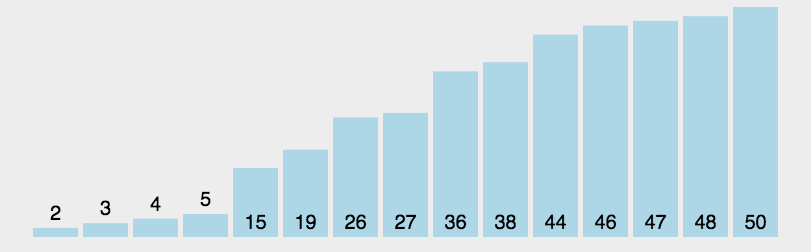
Example
Here's an implementation of Quick Sort in Python:
# Function to handle partitioning the array
def partition(arr, low, high):
i = (low - 1) # Index of smaller element
pivot = arr[high] # Pivot element
for j in range(low, high):
# If current element is smaller than or equal to pivot
if arr[j] <= pivot:
i = i + 1 # Increment index of smaller element
arr[i], arr[j] = arr[j], arr[i] # Swap
arr[i + 1], arr[high] = arr[high], arr[i + 1] # Swap the pivot
return i + 1
# Quick Sort function
def quickSort(arr, low, high):
if low < high:
# pi is the partitioning index
pi = partition(arr, low, high)
# Recursively sort the sub-arrays
quickSort(arr, low, pi - 1)
quickSort(arr, pi + 1, high)
# Example array
arr = [10, 7, 8, 9, 1, 5]
n = len(arr)
quickSort(arr, 0, n - 1)
# Print the sorted array
print("Sorted array:")
for i in range(n):
print("%d" % arr[i])Output:
Sorted array: 1 5 7 8 9 10
In this example, the array [10, 7, 8, 9, 1, 5] is sorted using the Quick Sort algorithm, with the final sorted array being [1, 5, 7, 8, 9, 10]. The pivot selection and partitioning play a key role in how efficiently the array gets sorted.



