In modern computer science and programming, algorithm efficiency is critically important. It not only affects program runtime but also directly relates to memory usage. To evaluate and optimize algorithms, two primary metrics are commonly used: time complexity and space complexity. This article introduces these concepts in detail and illustrates their practical applications with examples in C language.

1. Fundamentals of Algorithm Efficiency

When designing algorithms, two levels of objectives are pursued:

1. Finding a solution: The algorithm must reliably find the correct solution within the given input range.

2. Seeking an optimal solution: There may be multiple solutions to the same problem, but the goal is to find the most efficient algorithm.

Thus, algorithm efficiency has become the primary criterion for evaluating an algorithm’s quality, measured across two dimensions:

• Time efficiency: The speed of the algorithm’s execution.

• Space efficiency: The memory usage of the algorithm.

In essence, the goal is to design data structures and algorithms that are both "fast and space-saving." Evaluating time and space efficiency helps select suitable algorithms for specific problems and optimize program performance. The key metrics for these evaluations are time complexity and space complexity.

---

2. Time Complexity

2.1 Concept

Time complexity measures how the execution time of an algorithm changes as the input size grows. It helps evaluate the performance of algorithms, particularly when handling large data sets. Time complexity is usually expressed using Big O notation, which describes the worst-case runtime of the algorithm.

Rules for Deriving Big O

1. Retain only the highest-order term in the time complexity function $T(N)$, as lower-order terms become negligible as $N$ increases.

2. Remove constant coefficients from the highest-order term since their impact diminishes with large $N$.

3. If $T(N)$ contains no terms related to $N$, replace all constant terms with $O(1)$.

---

2.2 Common Types of Time Complexity

1. O(1) — Constant TimeConstant time complexity means the algorithm's runtime is independent of the input size $n$.

   // Constant Time Example
   int constant(int n) {
       int count = 0;
       int size = 100000;
       for (int i = 0; i < size; i++) {
           count++;
       }
       return count;
   }

2. O(n) — Linear TimeLinear time complexity means the runtime grows proportionally with the input size $n$. This often occurs in single loops.

   // Linear Time Example
   int linear(int n) {
       int count = 0;
       for (int i = 0; i < n; i++) {
           count++;
       }
       return count;
   }

   Array traversal or linked list traversal are typical examples:

   // Linear Time (Array Traversal)
   int arrayTraversal(int* nums, int n) {
       int count = 0;
       for (int i = 0; i < n; i++) {
           count++;
       }
       return count;
   }

3. O(n²) — Quadratic TimeQuadratic time complexity means the runtime grows quadratically with the input size $n$. This usually occurs in nested loops.

   // Quadratic Time Example
   int quadratic(int n) {
       int count = 0;
       for (int i = 0; i < n; i++) {
           for (int j = 0; j < n; j++) {
               count++;
           }
       }
       return count;
   }

4. O(2ⁿ) — Exponential TimeExponential time complexity means the runtime grows exponentially with the input size $n$. An example is solving combinatorial problems or deep recursive algorithms.

   
   

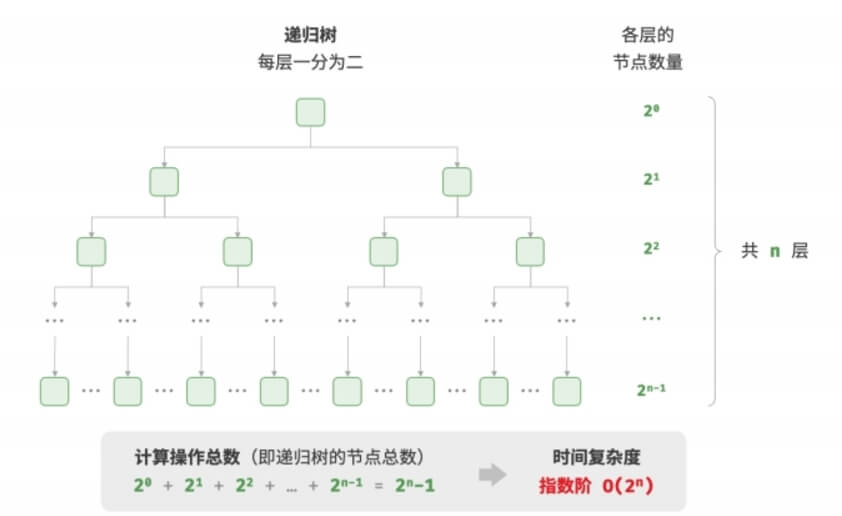
   // Exponential Time Example
   int expRecur(int n) {
       if (n == 1)
           return 1;
       return expRecur(n - 1) + expRecur(n - 1) + 1;
   }

5. O(log n) — Logarithmic TimeLogarithmic time complexity means the runtime grows logarithmically with the input size $n$. This often occurs in recursive functions where the input size is halved at each step.

   
   

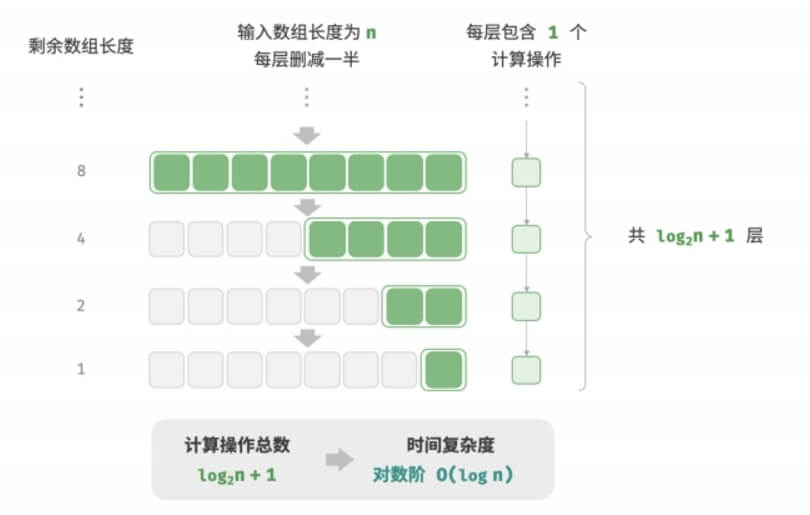
   // Logarithmic Time Example
   int logRecur(int n) {
       if (n <= 1)
           return 0;
       return logRecur(n / 2) + 1;
   }

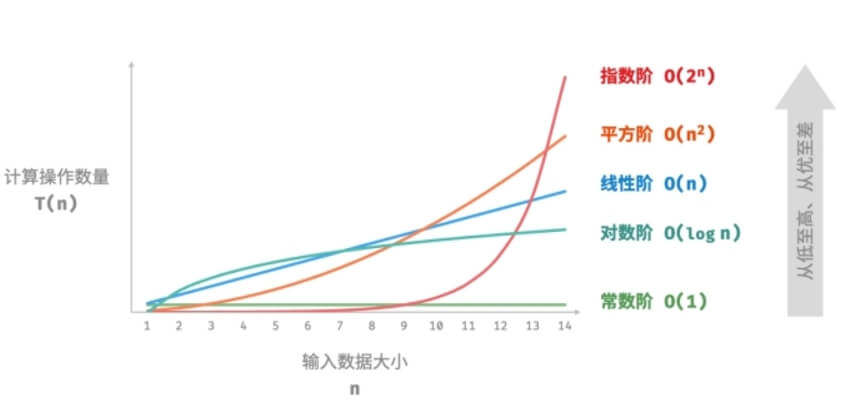
2.3 Common Big O Types in Ascending Order of Complexity

• $O(1)$ < $O(\log n)$ < $O(n)$ < $O(n \log n)$ < $O(n²)$ < $O(2^n)$ < $O(n!)$

Each step represents a significant increase in runtime as input size $n$ grows.

---

3. Space Complexity

3.1 Concept

Space Complexity measures how the additional memory required by an algorithm changes with the size of the input. It describes the memory demand of the algorithm and is commonly expressed using Big O notation. This concept is similar to time complexity, but with "runtime" replaced by "memory usage."

3.2 Common Types of Space Complexity

1. O(1) — Constant Space Complexity
   Constant space complexity means the additional memory required by the algorithm does not change with the size of the input. For example, swapping the values of two variables:

   #include <stdio.h>
   
   void swap(int *a, int *b) {
       int temp = *a;
       *a = *b;
       *b = temp;
   }
   
   int main() {
       int x = 10, y = 20;
       swap(&x, &y);
       printf("x = %d, y = %d\n", x, y);
       return 0;
   }

2. O(n) — Linear Space Complexity
   Linear space complexity indicates that the additional memory required grows proportionally with the input size. For instance, creating an array:

   #include <stdio.h>
   #include <stdlib.h>
   
   int *create_array(int size) {
       int *arr = (int *)malloc(size * sizeof(int));
       for (int i = 0; i < size; i++) {
           arr[i] = i;
       }
       return arr;
   }
   
   int main() {
       int size = 5;
       int *arr = create_array(size);
       for (int i = 0; i < size; i++) {
           printf("%d ", arr[i]);
       }
       printf("\n");
       free(arr);
       return 0;
   }

3. O(n²) — Quadratic Space Complexity
   Quadratic space complexity implies that the additional memory required grows proportionally to the square of the input size. For example, creating a 2D matrix:

   #include <stdio.h>
   #include <stdlib.h>
   
   int **create_matrix(int n) {
       int **matrix = (int **)malloc(n * sizeof(int *));
       for (int i = 0; i < n; i++) {
           matrix[i] = (int *)malloc(n * sizeof(int));
       }
       return matrix;
   }
   
   void print_matrix(int **matrix, int n) {
       for (int i = 0; i < n; i++) {
           for (int j = 0; j < n; j++) {
               printf("%d ", matrix[i][j]);
           }
           printf("\n");
       }
   }
   
   int main() {
       int n = 3;
       int **matrix = create_matrix(n);
       for (int i = 0; i < n; i++) {
           for (int j = 0; j < n; j++) {
               matrix[i][j] = i * n + j + 1;
           }
       }
       print_matrix(matrix, n);
       for (int i = 0; i < n; i++) {
           free(matrix[i]);
       }
       free(matrix);
       return 0;
   }

---

4. Conclusion

Understanding time complexity and space complexity is essential for writing efficient programs. While time complexity describes how an algorithm's runtime changes with input size, space complexity explains the memory requirements. Mastering these concepts allows developers to select and optimize algorithms effectively, improving program performance.

I hope this article helps you better understand algorithm complexity. If you have any questions or would like to discuss further, feel free to leave a comment!