No matter what kind of code you write, it will eventually be executed by the CPU. Therefore, if you want to write high-performance code, the techniques mentioned in this article are definitely worth studying seriously. Additionally, don’t think that this information is useless; it is very valuable. Over a decade ago, this knowledge greatly assisted me in performance tuning, allowing me to outpace many others…
Basic Knowledge
First, we all know that modern CPUs utilize multi-core technology and have multiple levels of cache. Older CPUs typically have two levels of memory (L1 and L2), while newer CPUs have three levels of memory (L1, L2, and L3), as shown in the diagram below:
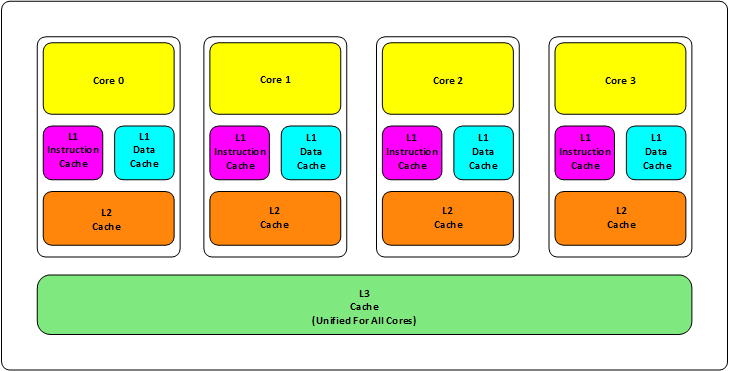
L1 Cache is divided into two types: instruction cache and data cache.
L2 and L3 Cache do not distinguish between instructions and data.
L1 and L2 caches exist within each CPU core, while L3 is shared among all CPU cores.
The closer L1, L2, and L3 caches are to the CPU, the smaller and faster they are; conversely, the farther away, the slower they become.
Next in the hierarchy is the RAM, followed by the hard disk. Let’s look at their access speeds:
L1 access speed: 4 CPU clock cycles
L2 access speed: 11 CPU clock cycles
L3 access speed: 39 CPU clock cycles
RAM access speed: 107 CPU clock cycles
We can see that L1 speed is 27 times faster than RAM; however, the sizes of L1 and L2 caches are generally in the KB range, while L3 is in the MB range. For example, the Intel Core i7-8700K is a 6-core CPU, where each core has L1 cache of 64KB (32KB for data and 32KB for instructions), L2 cache of 256KB, and L3 cache of 2MB (my Apple computer has an Intel Core i9-8950HK, which has the same cache sizes as the Core i7-8700K).
Our data flows from memory to L3, then to L2, then to L1, and finally to registers for CPU computation. Why is the design structured in three layers? Here are several considerations:
Physical Speed: A larger capacity requires more transistors. Besides increasing the chip size, a large number of transistors can lead to speed degradation, as the access speed is inversely proportional to the location of the transistors being accessed. In other words, when the signal path lengthens, communication speed slows down. This is a physical problem.
Data Synchronization: In multi-core technology, the state of data needs to be synchronized across multiple CPUs. The speed disparity between cache and RAM is significant; hence, having multiple levels of different-sized caches is beneficial for improving overall performance.
The world is always balanced; as one side becomes more glamorous, the other side will become darker. Establishing so many levels of cache introduces other problems, with two key issues:
A relatively straightforward issue: the cache hit rate.
A more complex issue: cache update consistency.
The second issue, particularly in multi-core technology, resembles distributed systems, where updates need to be made in multiple locations.
Cache Hits
Before addressing these two issues, we need to explain the term Cache Line. Cache essentially loads data into a location closer to itself. For the CPU, it does not load data byte by byte, as this is highly inefficient. Typically, data is loaded in chunks, and this chunk size is referred to as a "Cache Line." Generally, a mainstream CPU's Cache Line is 64 bytes (some CPUs use 32 bytes or 128 bytes). Thus, 64 bytes equals 16 32-bit integers, making it the smallest data unit that the CPU retrieves from memory.
For example: If the Cache Line is the smallest unit (64 bytes), then we first distribute the cache across multiple Cache Lines. For instance, if L1 is 32KB, then 32KB / 64B = 512 Cache Lines.
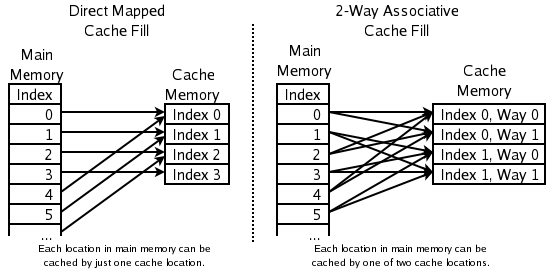
On one hand, the cache needs to bring data from memory, a process referred to as CPU Associativity. The strategy for placing cache data determines where data blocks from memory will be copied in the CPU cache. Because the cache size is much smaller than memory, there needs to be an address mapping algorithm that allows memory data to be mapped to the cache. This is somewhat similar to the method of mapping logical addresses to physical addresses but is not entirely the same.
Generally, we have the following methods:
Fully Associative Cache: Any memory address's data can be cached in any Cache Line. This method is the most flexible; however, if we want to know whether a memory address exists in the cache, we need to perform an O(n) complexity cache traversal, which is highly inefficient.
Hash Table Structure: To reduce cache search algorithm complexity, we can use data structures like hash tables. The simplest hash table performs a "modulus operation." For instance, if our L1 cache has 512 Cache Lines, the formula: (memory address mod 512) * 64 can directly find the offset of the Cache address. However, this approach requires our program to access memory addresses very evenly; otherwise, conflicts can become severe, making this an ideal situation.
To avoid the issues of the above two approaches, we need to tolerate some hash collisions, which leads to N-Way Set Associativity. This means grouping consecutive N Cache Lines, then first finding the related group and subsequently finding the relevant Cache Line within that group.
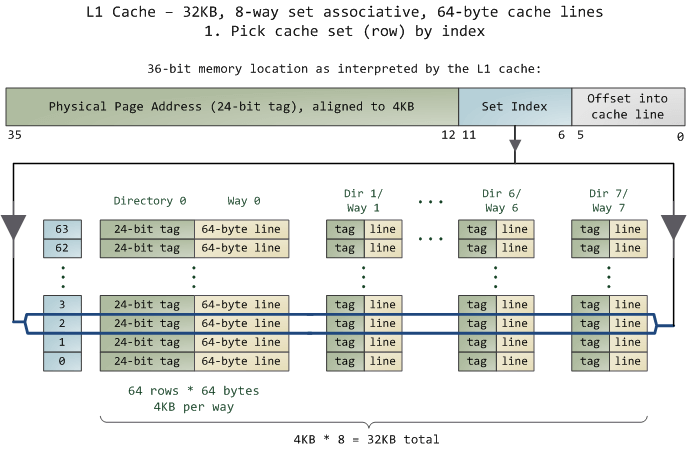
For N-Way set associativity, it might be somewhat difficult to understand, so here’s an example with more details (so that you can comprehend the subsequent code). Most Intel processors have L1 caches of 32KB with 8-Way set associativity, and each Cache Line is 64 bytes. This means:
32KB can be divided into 32KB / 64 = 512 Cache Lines.
Since it is 8-way, each way has 512 / 8 = 64 Cache Lines.
Thus, each way has 64 x 64 = 4096 bytes of memory.
To facilitate memory address indexing:
Tag: Each Cache Line has an independently allocated 24 bits for the tag, which stores the first 24 bits of the memory address.
Index: The next 6 bits of the memory address serve as the Cache Line index within this way, allowing for 2^6 = 64, which precisely indexes 64 Cache Lines.
Offset: The next 6 bits are used to represent the offset within the Cache Line.
https://manybutfinite.com/post/intel-cpu-caches/
When accessing a memory address, we first retrieve the middle 6 bits to find out which set it belongs to.
Then, within this 8-way cache line, we perform an O(n) search (where n=8) primarily to match the first 24 bits of the tag. If a match is found, it is considered a hit; if not, it is a cache miss, and if it’s a read operation, access must proceed to the next cache level. The algorithms for L2 and L3 caches are similar. There are two eviction algorithms: one is random, and the other is LRU (Least Recently Used). Nowadays, LRU is generally used (achieved by increasing an access counter).
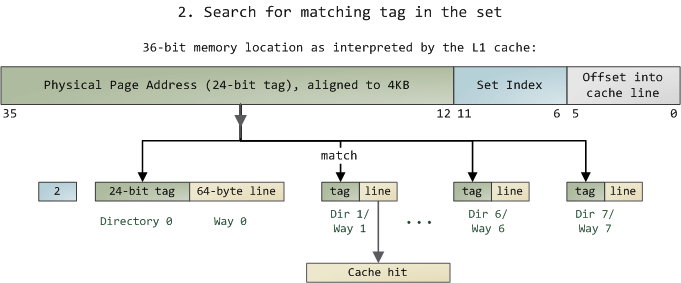
This also implies that:
L1 Cache can map a 36-bit memory address, totaling 2^36 = 64GB of memory.
When the CPU needs to access memory, it identifies which set through the middle 6 bits and locates the corresponding Cache Line using the first 24 bits.
Like a hash table structure, this leads to an O(1) index, followed by conflict searching. Because the middle 6 bits determine the same set, every 4096 bytes of continuous memory will be placed in the same group, causing cache conflicts.
Moreover, when data misses the cache, the CPU updates memory using a minimum of a Cache Line unit. Of course, the CPU doesn’t necessarily update just 64 bytes since accessing main memory is quite slow, so generally, more data will be updated. A good CPU employs some predictive techniques; if it identifies a pattern, it will preload additional memory, including instructions. This is referred to as Prefetching Technology (see Wikipedia's Cache Prefetching and the State University of New York's Memory Prefetching). For instance, if you are accessing a contiguous array in a for-loop with a fixed step size, memory can effectively prefetch.
Understanding these details helps us know under what circumstances cache misses can occur.
Cache Consistency
For mainstream CPUs, there are essentially two strategies for cache write operations (refer to our site’s article on "Cache Update Techniques"):
Write Back: Write operations occur only in the cache and are then flushed to memory.
Write Through: Write operations are performed simultaneously in both the cache and memory.
To improve write performance, mainstream CPUs (such as Intel Core i7/i9) generally adopt the Write Back strategy because writing directly to memory is significantly slower.
Now, the problem arises: if a data item is updated in the cache of CPU core 0, then the values of in other CPU cores must also be updated. This is the issue of cache consistency. (Of course, for the higher-level programs, we do not need to worry about how the caches of multiple CPU cores are synchronized; this is transparent to the upper-level code.)
Generally, there are two methods in CPU hardware to address this problem:
Directory Protocol: This method typically involves designing a centralized controller, which is part of the main memory controller. A directory is stored in the main memory containing global state information about the contents of various local caches. When a single CPU cache issues a read or write request, this centralized controller checks and issues the necessary commands for data synchronization and transfer between the main memory and CPU caches or among the CPU caches themselves.
Snoopy Protocol: This protocol resembles a bus-based notification system. CPU caches can recognize the data state on other caches through this protocol. If there is shared data, the state of that shared data can be communicated to other CPU caches via a broadcasting mechanism. This protocol requires each CPU cache to be able to "snoop" notifications of data events and respond accordingly. As illustrated below, there is a Snoopy Bus.
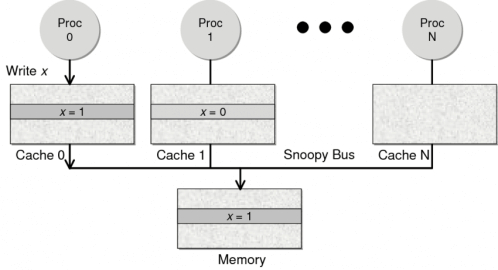
The Directory protocol is centralized, which can lead to performance bottlenecks and increase overall design complexity. On the other hand, the Snoopy protocol operates more like microservices with message communication, so currently, the design predominantly employs the Snoopy bus.
I would like to elaborate on some details here, as these micro-level concepts naturally connect to distributed systems. In distributed systems, we typically use distributed consistency algorithms such as Paxos or Raft. However, in the microcosm of the CPU, there is no need for such algorithms because the hardware of multiple CPU cores does not need to consider issues of network disconnections or delays. Thus, the core of synchronizing caches among multiple CPU cores is simply managing the state of the data.
Let’s introduce a few state protocols, starting with the simplest one, the MESI protocol. This protocol has no relation to the famous football player Messi; it mainly indicates that cached data has four states: Modified (M), Exclusive (E), Shared (S), and Invalid (I).
The state machine for these states is illustrated below (it’s a bit complex; you can skip it for now. This diagram simply aims to show how complex state control can be):
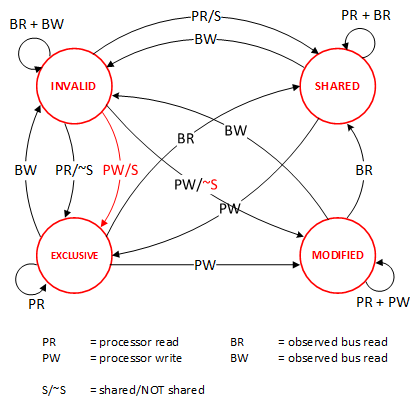
Here’s an example (if you want to see an animated demonstration, there is a webpage [MESI Interactive Animations] where you can interactively operate; the animation uses the Write Through algorithm):
| Current Operation | CPU0 | CPU1 | Memory | Description |
|---|---|---|---|---|
| 1) CPU0 read(x) | x=1 (E) | x=1 | x=1 | Only one CPU has the variable x, so the state is Exclusive |
| 2) CPU1 read(x) | x=1 (S) | x=1 (S) | x=1 | Both CPUs read the variable x, changing the state to Shared |
| 3) CPU0 write(x,9) | x=9 (M) | x=1 (I) | x=1 | The variable changes; state in CPU0 becomes Modified; in CPU1, it becomes Invalid |
| 4) Variable x written back to memory | x=9 (M) | x=1 (I) | x=9 | Current state remains unchanged |
| 5) CPU1 read(x) | x=9 (S) | x=9 (S) | x=9 | Variable synchronizes across all caches, returning state to Shared |
In the MESI protocol, after data is updated, other shared CPU caches’ copies of that data are marked as Invalid, causing a cache miss when other CPUs read again. Updating data from memory means a slowdown of 20 times. Can we update directly from the neighboring CPU cache? Yes, this can significantly speed up operations, but state control becomes more complex. We need to introduce an additional state: Owner (O), to indicate that I am the source updating the data. Thus, the MOESI protocol emerged.
I won’t provide the state machine and demonstration example for the MOESI protocol (you can check related course materials at Berkeley if you’re interested), but we only need to understand that the MOESI protocol allows for data synchronization among CPU caches, thereby reducing memory operations and greatly enhancing performance, though the control logic becomes quite complex.
For your reference, a protocol similar to MOESI is MESIF, where F stands for Forward. It similarly forwards updated data to other CPU caches; however, the data in the Owner state of MOESI is dirty and has not been written back to memory, while the data in the Forward state of MESIF is clean and can be discarded without further notification.
It’s worth noting that AMD uses MOESI, while Intel uses MESIF. Hence, the F state is mainly designed for CPU L3 Cache (as mentioned earlier, L3 is shared among all CPU cores). (For relevant comparisons, you can refer to answers on this question on StackOverflow.)
Program Performance
Having understood the above concepts, let's examine their impact on program performance.
Example 1
First, let's assume we have an array of length 64M. Consider the following two loops:
const int LEN = 64 * 1024 * 1024; int *arr = new int[LEN]; for (int i = 0; i < LEN; i += 2) arr[i] *= i; for (int i = 0; i < LEN; i += 8) arr[i] *= i;
In theory, the second loop should have four times less computational work and be four times faster. However, when I ran it on my machine, the first loop took 127 milliseconds, while the second loop took 121 milliseconds—barely any difference. The main reason for this is the Cache Line, as the CPU loads in minimum units of a Cache Line, which is 64 Bytes, equivalent to 16 32-bit integers. Therefore, regardless of whether the stride is 2 or 8, the performance remains similar. Moreover, the subsequent multiplication operation does not consume much CPU time.
Example 2
Next, let's look at some code related to cache hit rates, where we access a contiguous array with a certain increment:
for (int i = 0; i < 10000000; i++) {
for (int j = 0; j < size; j += increment) {
memory[j] += j;
}
}Let's test this. In the following table, the header indicates the step size (i.e., how many integers to skip each time), while the vertical axis shows how many times the array can be accessed (you can interpret this as how many Cache Lines are involved). Each entry in the table represents the array size and step size. For instance, if the horizontal axis is 512 and the vertical axis is 4, it means the array has in length, accessed with a step of 512, which corresponds to these items: [0, 512, 1024, 1536].
The same entries show the time for running the loop 10 million times, measured in microseconds (divided by 1000 gives milliseconds).
| Count | 1 | 16 | 512 | 1024 |
|---|---|---|---|---|
| 1 | 17539 | 16726 | 15143 | 14477 |
| 2 | 15420 | 14648 | 13552 | 13343 |
| 3 | 14716 | 14463 | 15086 | 17509 |
| 4 | 18976 | 18829 | 18961 | 21645 |
| 5 | 23693 | 23436 | 74349 | 29796 |
| 6 | 23264 | 23707 | 27005 | 44103 |
| 7 | 28574 | 28979 | 33169 | 58759 |
| 8 | 33155 | 34405 | 39339 | 65182 |
| 9 | 37088 | 37788 | 49863 | 156745 |
| 10 | 41543 | 42103 | 58533 | 215278 |
| 11 | 47638 | 50329 | 66620 | 335603 |
| 12 | 49759 | 51228 | 75087 | 305075 |
| 13 | 53938 | 53924 | 77790 | 366879 |
| 14 | 58422 | 59565 | 90501 | 466368 |
| 15 | 62161 | 64129 | 90814 | 525780 |
| 16 | 67061 | 66663 | 98734 | 440558 |
| 17 | 71132 | 69753 | 171203 | 506631 |
| 18 | 74102 | 73130 | 293947 | 550920 |
We can see that after [9, 1024], the time significantly increases. This includes [17, 512] and [18, 512], which also show significant increases. The reason is that my machine's L1 Cache is 32KB, 8-Way. As mentioned earlier, 8-Way has 64 sets, each with 8 Cache Lines. When the for-loop stride exceeds 1024 integers (which is exactly 4096 Bytes), the memory address changes mainly in the high-order 24 bits, while the low-order 12 bits change little, especially the middle 6 bits remaining unchanged. This causes all accesses to hit the same set, leading to numerous cache conflicts, which degrade performance and increase time. The same goes for [16, 512], where a few steps start causing L1 Cache conflicts and failures.
Example 3
Now let's look at another example. Below are two methods for traversing a two-dimensional array: one row-wise and the other column-wise. Theoretically, both methods should have the same addressing and computational load, and their execution times should also be similar.
const int row = 1024;
const int col = 512;
int matrix[row][col];
// Row-wise traversal
int sum_row = 0;
for (int _r = 0; _r < row; _r++) {
for (int _c = 0; _c < col; _c++) {
sum_row += matrix[_r][_c];
}
}
// Column-wise traversal
int sum_col = 0;
for (int _c = 0; _c < col; _c++) {
for (int _r = 0; _r < row; _r++) {
sum_col += matrix[_r][_c];
}
}However, that's not the case. On my machine, I obtained the following results:
Row-wise traversal: 0.081ms
Column-wise traversal: 1.069ms
There's a significant difference in execution time. The reason is that column-wise traversal is not friendly to CPU Cache operation, resulting in a huge performance cost.
Example 4
Next, let's look at performance issues in a multi-core environment with the following code. Two threads operate on two different elements of an array (no locking required), looping 10 million times to perform addition operations. In the code below, I've highlighted one line: the p2 pointer, which can either be p[1] or p[30]. Theoretically, accessing any two elements of the array should yield similar execution times.
void fn(int* data) {
for (int i = 0; i < 10 * 1024 * 1024; ++i)
*data += rand();
}
int p[32];
int *p1 = &p[0];
int *p2 = &p[1]; // int *p2 = &p[30];
thread t1(fn, p1);
thread t2(fn, p2);However, this was not the case on my machine:
For
p[0]andp[1]: 560msFor
p[0]andp[30]: 104ms
This discrepancy arises because p[0] and p[1] are on the same Cache Line, while p[0] and p[30] cannot be on the same Cache Line. The smallest update unit for the CPU cache is the Cache Line, which means that even though the two threads are writing different data, since both data points reside on the same Cache Line, it leads to constant synchronization between the L1/L2 caches of the two CPUs, causing a 5-fold difference in execution time.
Example 5
Finally, let's look at another piece of code: we want to count the number of odd numbers in a large array. To speed up the processing, we hope to use multithreading. In the following code, we pass an ID to each thread, which is then used to perform the counting task on the corresponding segment of the array.
int total_size = 16 * 1024 * 1024; // Array length
int* test_data = new int[total_size]; // Array
int nthread = 6; // Number of threads (since my machine is 6-core)
int result[nthread]; // Array to collect results
void thread_func(int id) {
result[id] = 0;
int chunk_size = total_size / nthread + 1;
int start = id * chunk_size;
int end = min(start + chunk_size, total_size);
for (int i = start; i < end; ++i) {
if (test_data[i] % 2 != 0) ++result[id];
}
}However, during execution, you will find that the six threads run slower than one thread. As we learned from the previous examples, the data in the result[] array exists within the same Cache Line, so all threads continuously perform write operations on this Cache Line. This leads to constant re-synchronization of the Cache Line where result[] resides, causing the performance of six threads to be worse than that of a single thread. This phenomenon is called False Sharing.
The optimization is straightforward: use a thread-local variable.
void thread_func(int id) {
result[id] = 0;
int chunk_size = total_size / nthread + 1;
int start = id * chunk_size;
int end = min(start + chunk_size, total_size);
int c = 0; // Using a temporary variable, no cache line synchronization
for (int i = start; i < end; ++i) {
if (test_data[i] % 2 != 0) ++c;
}
result[id] = c;
}We run both programs with 1 to 32 threads and plot the results as shown below (the x-axis is the number of threads, and the y-axis is the time taken to complete the count, measured in microseconds):
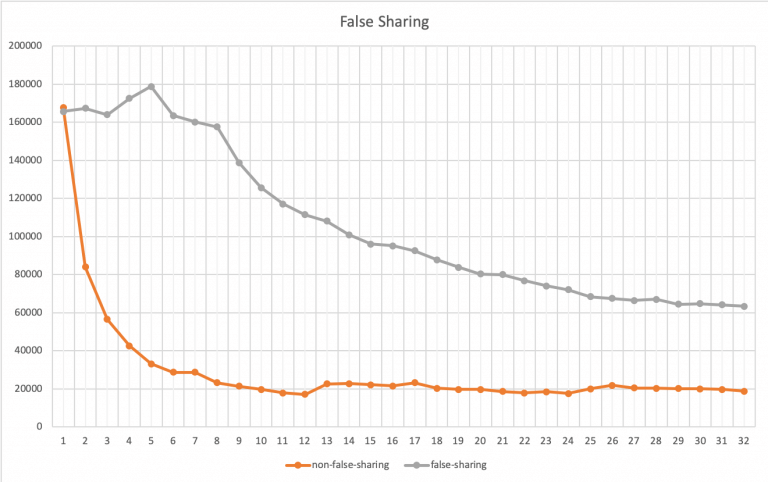
In the graph, the gray curve represents the first method, while the orange curve represents the second (using local variables). When there is only one thread, the two methods are comparable, showing little difference. However, as the number of threads increases, you will notice that the performance of the second method improves significantly. It stabilizes when reaching six threads (as mentioned, my CPU is 6-core). No matter how many threads are added, the first method cannot outperform the second method. This is because the first method is not friendly to CPU Cache. In other words, as long as the number of CPU cores is sufficient, the second method can achieve linear performance scaling, allowing each CPU core to run concurrently, while the first method cannot.
Due to space constraints, I will conclude the examples here. For related code, please refer to my GitHub repository.
Further Reading
Wikipedia: CPU Cache
Classic Article: Gallery of Processor Cache Effects (Although the tests in this article are somewhat outdated, the concepts discussed remain highly applicable.)
Effective C++ Author Scott Meyers' Talk: CPU Caches and Why You Care (YouTube, PPT)
Textbook from Swarthmore College: Cache Architecture and Design
Classic Article: What Every Programmer Should Know About Memory (This article is very classic, but the introduction is a bit obscure, as it delves into transistor structures; chapters three and six are the key points.)
A code repository on GitHub: hardware-effects, featuring demonstrations of programs affected by the CPU
Classic Data: Latency Numbers Every Programmer Should Know
For Java, you can check out this article: Optimizing Memory Access With CPU Cache or Writing Cache-Friendly Code.
In summary, CPU cache optimization techniques are not new; just Google it, and you'll find plenty of articles...