Topological Sorting of a Directed Acyclic Graph (DAG)

Topological sorting of a Directed Acyclic Graph (DAG) involves arranging all the vertices in a linear sequence such that for every directed edge $(u, v)$ in the graph, vertex $u$ appears before vertex $v$ in the sequence. Such a linear sequence is called a topological order, or simply a topological sequence. In simpler terms, topological sorting is the process of obtaining a total order from a partial order defined on a set.

In graph theory, a sequence of vertices of a directed acyclic graph is called a topological sorting if and only if it satisfies the following conditions:

1. Each vertex appears exactly once.

2. If vertex $A$ precedes vertex $B$ in the sequence, then there is no path from $B$ to $A$ in the graph.

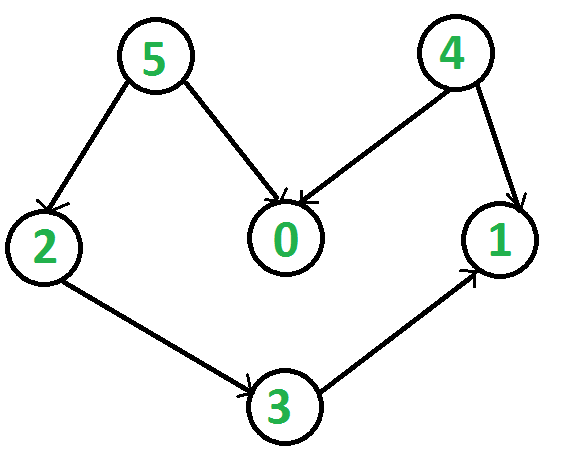
Example:

from collections import defaultdict

class Graph:
    def __init__(self, vertices):
        self.graph = defaultdict(list)
        self.V = vertices

    def addEdge(self, u, v):
        self.graph[u].append(v)

    def topologicalSortUtil(self, v, visited, stack):
        visited[v] = True

        for i in self.graph[v]:
            if not visited[i]:
                self.topologicalSortUtil(i, visited, stack)

        stack.insert(0, v)

    def topologicalSort(self):
        visited = [False] * self.V
        stack = []

        for i in range(self.V):
            if not visited[i]:
                self.topologicalSortUtil(i, visited, stack)

        print(stack)

# Create a graph and add edges
g = Graph(6)
g.addEdge(5, 2)
g.addEdge(5, 0)
g.addEdge(4, 0)
g.addEdge(4, 1)
g.addEdge(2, 3)
g.addEdge(3, 1)

print("Topological Sorting Result:")
g.topologicalSort()

Output:

Topological Sorting Result:
[5, 4, 2, 3, 1, 0]

In this example, the graph is represented by the vertices and directed edges, and the topological sorting function outputs a valid topological order of the vertices. The result [5, 4, 2, 3, 1, 0] indicates a sequence where each directed edge $u \rightarrow v$ respects the order $u$ before $v$.