Unlocking the Charm of Binary Trees: A Detailed Explanation of Linked Implementations

Time： 2024-11-21 Column：AI views：207

In the vast universe of data structures, the binary tree is like a brilliant gem, with its elegant structure and powerful functionality making it an indispensable tool in computer science. From database indexing to compiler syntax trees, binary trees uniquely support many core algorithms and data processing tasks. This article will delve into how to implement binary trees using C language in a linked structure and provide a detailed explanation of each part of the implementation.

1. Structure of a Binary Tree

1.1 Structure

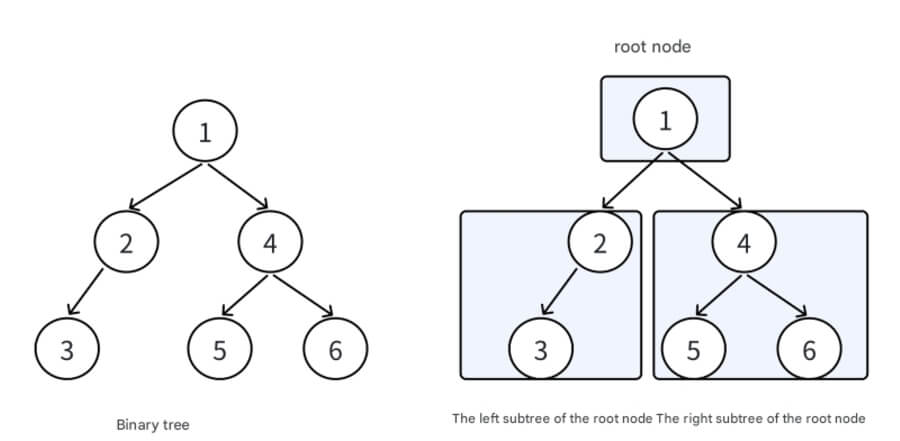
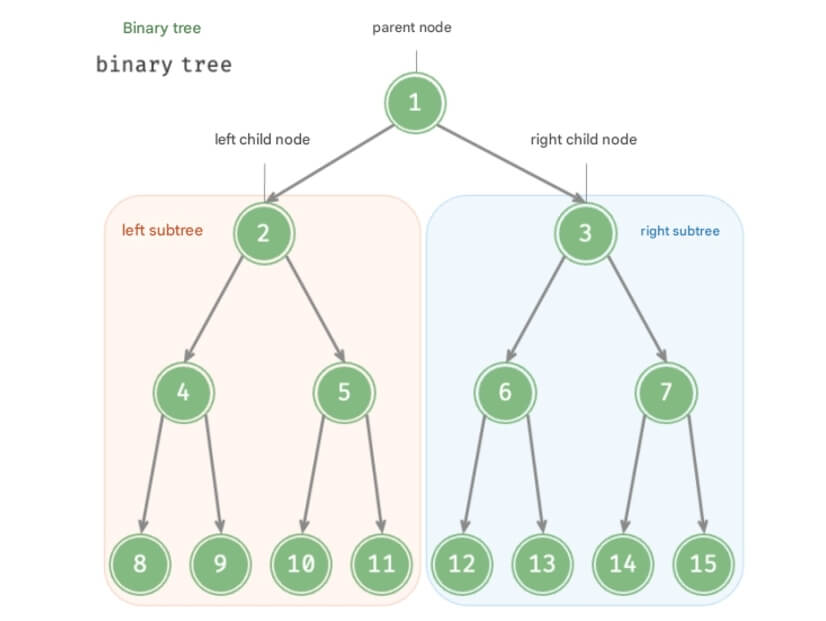
A binary tree is a nonlinear data structure that represents the derived relationship between "ancestors" and "descendants," reflecting the "divide and conquer" logic. Similar to a linked list, the basic unit of a binary tree is a node, each containing a value and references to left and right child nodes.

// Binary tree node structure
typedef int DataType;
typedef struct BinaryTreeNode
{
    int data;                   // Data field
    struct BinaryTreeNode* left; // Pointer to the left child node
    struct BinaryTreeNode* right; // Pointer to the right child node
} BTNode;

Each node has two references (pointers), pointing to the left child node and the right child node. This node is referred to as the parent node of these two child nodes. When given a binary tree node, the subtree formed by the left child node and its descendants is called the left subtree, and similarly, the right subtree is formed by the right child node.

Unlocking the Charm of Binary Trees: A Detailed Explanation of Linked Implementations

1.2 Advantages of Linked Implementation

There are several notable advantages of implementing a binary tree using linked structures:

Dynamic Size: Linked structures can dynamically allocate memory as needed, avoiding the fixed-size limitation and being suitable for handling uncertain amounts of data.
Space Efficiency: Linked structures only allocate memory for existing nodes, reducing space wastage, and are more efficient than array implementations.
Simplified Operations: Insertion and deletion operations do not require moving other elements, making them more efficient, and allowing the binary tree to perform well in data environments with frequent changes.

2. Basic Operations of a Binary Tree

Creating a binary tree can be relatively complex. To better understand binary trees, let's first manually create a linked binary tree:

BTNode* buyNode(DataType x)
{
    BTNode* newnode = (BTNode*)malloc(sizeof(BTNode));
    if (newnode == NULL)
    {
        perror("malloc fail!");
        exit(1);
    }
    newnode->data = x;
    newnode->left = newnode->right = NULL;
    return newnode;
}

BTNode* CreateTree()
{
    BTNode* n1 = buyNode(1);
    BTNode* n2 = buyNode(2);
    BTNode* n3 = buyNode(3);
    BTNode* n4 = buyNode(4);
    BTNode* n5 = buyNode(5);
    BTNode* n6 = buyNode(6);
    n1->left = n2;
    n1->right = n4;
    n2->left = n3;
    n4->left = n5;
    n4->right = n6;
    return n1;
}

2.1 Preorder Traversal

Preorder traversal is a depth-first traversal method where nodes are visited in the order "root -> left subtree -> right subtree." This method is crucial for copying tree structures or parsing expression trees.

Traversal Order:

Visit the current node (root).
Recursively visit the left subtree.
Recursively visit the right subtree.

Applications:

Generating serialized representations of trees.
Copying tree structures.
Constructing prefix expressions in expression trees.

Recursive Implementation:

// Preorder Traversal
// Visit order: root -> left subtree -> right subtree
void PreOrder(BTNode* root)
{
    if (root == NULL)
    {
        return;
    }
    printf("%d ", root->data);
    PreOrder(root->left);
    PreOrder(root->right);
}

In this implementation, we first check if the current node is null. If not, we print the node's data and then recursively visit the left and right child nodes. This order ensures that the root node is always visited first, which is effective for many applications.

2.2 Inorder Traversal

Inorder traversal is a depth-first traversal method where nodes are visited in the order "left subtree -> root -> right subtree." This traversal plays an essential role in generating ordered node sequences and parsing expression trees.

Traversal Order:

Recursively visit the left subtree.
Visit the current node (root).
Recursively visit the right subtree.

Applications:

Generating an ordered sequence of nodes.
Constructing infix expressions in expression trees.

Recursive Implementation:

// Inorder Traversal
// Visit order: left subtree -> root -> right subtree
void InOrder(BTNode* root)
{
    if (root == NULL)
    {
        return;
    }
    InOrder(root->left);
    printf("%d ", root->data);
    InOrder(root->right);
}

In this implementation, we recursively visit the left child node, then print the node’s data, and finally recursively visit the right child node. This order ensures that the nodes are visited in an ordered manner.

2.3 Postorder Traversal

Postorder traversal is a depth-first traversal method where nodes are visited in the order "left subtree -> right subtree -> root." This traversal is particularly useful when you need to process child nodes before the parent node.

Traversal Order:

Recursively visit the left subtree.
Recursively visit the right subtree.
Visit the current node (root).

Applications:

Calculating the height or size of a tree.
Deleting a tree structure, ensuring that child nodes are deleted first.
Constructing suffix expressions in expression trees.

Recursive Implementation:

// Postorder Traversal
// Visit order: left subtree -> right subtree -> root
void PostOrder(BTNode* root)
{
    if (root == NULL)
    {
        return;
    }
    PostOrder(root->left);
    PostOrder(root->right);
    printf("%d ", root->data);
}

In this implementation, we recursively visit the left and right child nodes first, then print the node’s data. This order ensures that all child nodes are processed before the parent node, suitable for reverse processing scenarios.

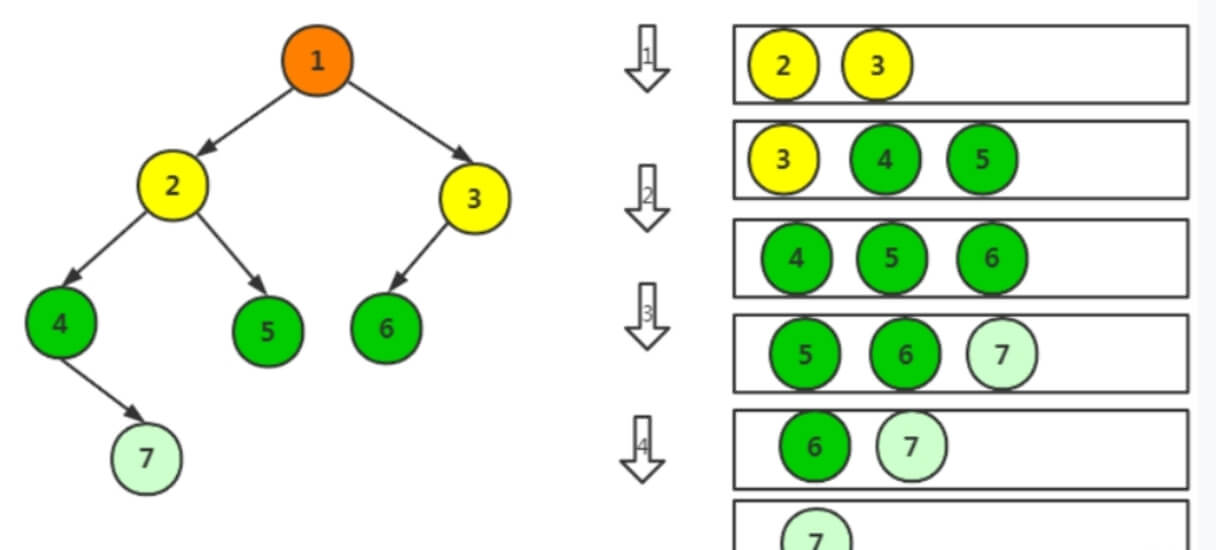
2.4 Level-order Traversal

Level-order traversal is a breadth-first traversal method where nodes are visited from "top to bottom, left to right." It is particularly useful in scenarios that require processing nodes layer by layer, such as printing the tree level by level or calculating the depth of the tree.

The steps are as follows:

Initialize a queue and enqueue the root node.
While the queue is not empty, repeat the following:

Dequeue a node and visit it (print or record).
Enqueue the left and right child nodes (if they exist).

Code Implementation:

// Level-order Traversal using Queue
void LevelOrder(BTNode* root)
{
    QU q; // Create a queue
    QueueInit(&q);
    QueuePush(&q, root); // Enqueue the root node, making it the front of the queue
    while (!QueueEmpty(&q)) // While the queue is not empty
    {
        BTNode* Qhead = QueueFront(&q);
        printf("%d ", Qhead->data);
        QueuePop(&q); // Dequeue the front node
        if (Qhead->left)
        {
            QueuePush(&q, Qhead->left); // Enqueue the left child node
        }
        if (Qhead->right)
        {
            QueuePush(&q, Qhead->right); // Enqueue the right child node
        }
    }
    QueueInit(&q);
    QueueDestroy(&q);
}

2.5 Calculate the Number of Nodes in a Binary Tree

The steps are as follows:

If the current node is null, return 0 (no nodes).
If the current node is not null, return 1 (for the current node) plus the number of nodes in the left and right subtrees.

Code Implementation:

int BTSize(BTNode* root)
{
    if (root == NULL)
    {
        return 0;
    }
    return BTSize(root->left) + BTSize(root->right) + 1;
}

2.6 Finding the Number of Leaf Nodes in a Binary Tree
Leaf Node: A node without children.
Non-leaf Node: A node with at least one child.
Steps are as follows:

If the current node is NULL, return 0 (no leaf nodes).
If the current node is a leaf node (both left and right children are NULL), return 1.
If the current node is not a leaf node, recursively calculate the number of leaf nodes in the left and right subtrees, and add the results.

Code Implementation:

// Binary tree leaf node count: Leaf nodes are nodes with degree 0
int BTLeafSize(BTNode* root)
{
    if (root == NULL)
    {
        return 0;
    }
    if (root->left == NULL && root->right == NULL)
    {
        return 1;
    }
    return BTLeafSize(root->left) + BTLeafSize(root->right);
}

2.7 Finding the Number of Nodes at the k-th Level of a Binary Tree
Steps are as follows:

If the current node is NULL, return 0.
If the current level equals k, return 1.
If the current level is less than k, recursively calculate the number of nodes at the k-th level in the left and right subtrees.

Code Implementation:

// Binary tree k-th level node count
int BTLevelKSize(BTNode* root, int k)
{
    if (root == NULL)
    {
        return 0;
    }
    if (k == 1)
    {
        return 1;
    }
    return BTLevelKSize(root->left, k - 1) + BTLevelKSize(root->right, k - 1);
}

2.8 Finding the Height of a Binary Tree
Steps are as follows:

If the current node is NULL, return 0 (the height of the tree is 0).
Recursively calculate the height of the left and right subtrees.
Return the larger of the heights of the left and right subtrees, plus 1 (representing the height of the current node).

Code Implementation:

// Binary tree depth/height
int BTDepth(BTNode* root)
{
    if (root == NULL)
    {
        return 0;
    }
    // Return the deeper of the left or right subtree
    return BTDepth(root->left) > BTDepth(root->right) ? BTDepth(root->left) + 1 : BTDepth(root->right) + 1;
}

2.9 Searching for a Value in a Binary Tree
Steps are as follows:

If the current node is NULL, return NULL (not found).
If the current node's value equals x, return the current node.
If the current node's value does not equal x, recursively search the left and right subtrees.
If found in the left subtree, return that node; otherwise, continue searching in the right subtree.

Code Implementation:

// Binary tree search for a node with value x
BTNode* BTFind(BTNode* root, DataType x)
{
    if (root == NULL)
    {
        return NULL;
    }
    if (root->data == x)
    {
        return root;
    }
    BTNode* leftFind = BTFind(root->left, x); // Search in the left subtree
    if (leftFind)
    {
        return leftFind; // Found in the left subtree, return
    }
    BTNode* rightFind = BTFind(root->right, x); // Search in the right subtree
    if (rightFind)
    {
        return rightFind; // Found in the right subtree, return
    }
    return NULL;
}

2.10 Checking if a Binary Tree is a Complete Binary Tree
Method Overview:

Queue Initialization: Use a queue for level-order traversal.
Traversal Process:

Enqueue the root node to begin traversal.
Dequeue a node from the queue and check if it is NULL.
For each non-null node, enqueue its left and right children.
Once an empty node is encountered, mark that all subsequent nodes must be NULL.
Final Verification: Continue traversing the queue to ensure all subsequent nodes are NULL.

Code Implementation:

// Check if a binary tree is a complete binary tree -- using a queue
bool BTComplete(BTNode* root)
{
    QU q; // Create a queue
    QueueInit(&q);
    QueuePush(&q, root); // Enqueue the root node

    while (!QueueEmpty(&q)) // While the queue is not empty
    {
        BTNode* Qhead = QueueFront(&q);
        QueuePop(&q);
        if (Qhead == NULL)
        {
            break;
        }
        QueuePush(&q, Qhead->left); // Enqueue left child
        QueuePush(&q, Qhead->right); // Enqueue right child
    }

    // Once an empty node is encountered, ensure all subsequent nodes are NULL
    while (!QueueEmpty(&q)) // While the queue is not empty
    {
        BTNode* Qhead = QueueFront(&q);
        QueuePop(&q);
        if (Qhead != NULL)
        {
            return false; // Found a non-null node, meaning it's not a complete binary tree
        }
    }

    QueueDestroy(&q);
    return true; // It's a complete binary tree
}

2.11 Destroying a Binary Tree
Code Implementation:

// Destroy binary tree  
// Post-order traversal: first destroy the left subtree, then the right subtree, and finally the root node
void BTDestroy(BTNode** root)
{
    if (*root == NULL)
    {
        return;
    }
    BTDestory(&((*root)->left)); // Destroy the left subtree
    BTDestory(&((*root)->right)); // Destroy the right subtree
    free(*root); // Free the root node
    *root = NULL;
}

Level-order Traversal using a Queue

// Level-order traversal using a queue
void LevelOrder(BTNode* root)
{
    QU q; // Create a queue
    QueueInit(&q);
    QueuePush(&q, root); // Enqueue the root node

    while (!QueueEmpty(&q)) // While the queue is not empty
    {
        BTNode* Qhead = QueueFront(&q);
        printf("%d ", Qhead->data); // Print the current node
        QueuePop(&q); // Dequeue the node

        // Enqueue the left child of the current node
        if (Qhead->left)
        {
            QueuePush(&q, Qhead->left);
        }

        // Enqueue the right child of the current node
        if (Qhead->right)
        {
            QueuePush(&q, Qhead->right);
        }
    }

    QueueInit(&q);
    QueueDestroy(&q);
}

3. Complete Code

Queue.h
Queue Declaration

#pragma once
#include<stdio.h>
#include<stdlib.h>
#include<assert.h>
#include<stdbool.h>
//typedef int DataType;
typedef struct BinaryTreeNode* QDataType;
// Define Node structure
typedef struct Node
{
    QDataType data;  // Data field
    struct Node* next;  // Pointer field
} Node;

// Define Queue structure
typedef struct Queue
{
    Node* phead;  // Queue head
    Node* ptail;  // Queue tail
    int size;  // Queue size
} QU;

// Initialize the queue
void QueueInit(QU* p);
// Enqueue, add to the tail
void QueuePush(QU* p, QDataType x);
// Check if the queue is empty
bool QueueEmpty(QU* p);
// Dequeue, remove from the head
void QueuePop(QU* p);
// Get the front data of the queue
QDataType QueueFront(QU* p);
// Get the back data of the queue
QDataType QueueBack(QU* p);
// Get the size of the queue
int QueueSize(QU* p);
// Destroy the queue
void QueueDestroy(QU* p);

Queue.c
Queue Definition

#define _CRT_SECURE_NO_WARNINGS
#include"Queue.h"

// Initialize the queue
void QueueInit(QU* p)
{
    assert(p);
    p->phead = p->ptail = NULL; // Initialize head and tail pointers as NULL
    p->size = 0; // Initialize queue size to 0
}

// Create a new node
Node* CreateNode(QDataType x)
{
    Node* newnode = (Node*)malloc(sizeof(Node));
    if (newnode == NULL) {
        perror("malloc fail");
        exit(1); // Exit the program if allocation fails
    }
    newnode->data = x;  // Set node data
    newnode->next = NULL; // Initialize next pointer as NULL
    return newnode; // Return the new node
}

// Enqueue operation (insert at the tail)
void QueuePush(QU* p, QDataType x)
{
    assert(p);
    Node* newnode = CreateNode(x);
    if (p->phead == NULL) // When the queue is empty
    {
        p->phead = p->ptail = newnode; // Set both head and tail pointers to the new node
    }
    else // When the queue is not empty
    {
        p->ptail->next = newnode; // Set the next pointer of the tail node to the new node
        p->ptail = newnode; // Update the tail pointer to the new node
    }
    ++p->size; // Increment the queue size
}

// Check if the queue is empty
bool QueueEmpty(QU* p)
{
    assert(p);
    return p->phead == NULL; // If head pointer is NULL, the queue is empty
}

// Dequeue operation (remove from the head)
void QueuePop(QU* p)
{
    assert(p);
    assert(!QueueEmpty(p)); // Ensure the queue is not empty
    if (p->phead == p->ptail) // When there is only one element
    {
        free(p->phead); // Free the head node
        p->phead = p->ptail = NULL; // Set both head and tail pointers to NULL
    }
    else
    {
        Node* del = p->phead; // Save the node to be deleted
        p->phead = p->phead->next; // Update the head pointer to the next node
        free(del); // Free the deleted node
    }
    --p->size; // Decrement the queue size
}

// Get the front data of the queue
QDataType QueueFront(QU* p)
{
    assert(p);
    assert(!QueueEmpty(p)); // Ensure the queue is not empty
    return p->phead->data; // Return the data of the head node
}

// Get the back data of the queue
QDataType QueueBack(QU* p)
{
    assert(p);
    assert(!QueueEmpty(p)); // Ensure the queue is not empty
    return p->ptail->data; // Return the data of the tail node
}

// Get the size of the queue
int QueueSize(QU* p)
{
    assert(p);
    return p->size; // Return the size of the queue
}

// Destroy the queue
void QueueDestroy(QU* p)
{
    assert(p);
    Node* pcur = p->phead;
    while (pcur) // Traverse all nodes and free memory
    {
        Node* next = pcur->next;
        free(pcur);
        pcur = next;
    }
    p->phead = p->ptail = NULL; // Set head and tail pointers to NULL
    p->size = 0; // Set the queue size to 0
}

Tree.h
Binary Tree Declaration

#pragma once
#include<stdio.h>
#include<assert.h>
#include<stdlib.h>
#include<stdbool.h>

// Define the binary tree linked structure
// Binary tree node structure
typedef int DataType;
typedef struct BinaryTreeNode
{
    int data; // Value field
    struct BinaryTreeNode* left; // Pointer to the left child
    struct BinaryTreeNode* right; // Pointer to the right child
} BTNode;

// Pre-order traversal -- root, left, right
void PreOrder(BTNode* root);
// In-order traversal -- left, root, right
void InOrder(BTNode* root);
// Binary tree node count
int BTSize(BTNode* root);
// Binary tree leaf node count
int BTLeafSize(BTNode* root);
// Binary tree node count at the k-th level
int BTLevelKSize(BTNode* root, int k);
// Binary tree depth/height
int BTDepth(BTNode* root);
// Find the node with value x in the binary tree
BTNode* BTFind(BTNode* root, DataType x);
// Destroy the binary tree
void BTDestroy(BTNode** root);
// Level-order traversal -- using a queue
void LevelOrder(BTNode* root);
// Check if the binary tree is a complete binary tree -- using a queue
bool BTComplete(BTNode* root);

Tree.c
Binary Tree Implementation

#define _CRT_SECURE_NO_WARNINGS
#include"Tree.h"
#include"Queue.h"

// Pre-order traversal
// Visit priority: root node -> left subtree -> right subtree
void PreOrder(BTNode* root)
{
    if (root == NULL)
    {
        return;
    }
    printf("%d ", root->data);
    PreOrder(root->left);
    PreOrder(root->right);
}

// In-order traversal
// Visit priority: left subtree -> root node -> right subtree
void InOrder(BTNode* root)
{
    if (root == NULL)
    {
        return;
    }
    InOrder(root->left);
    printf("%d ", root->data);
    InOrder(root->right);
}

// Post-order traversal
// Visit priority: left subtree -> right subtree -> root node
void PostOrder(BTNode* root)
{
    if (root == NULL)
    {
        return;
    }
    PostOrder(root->left);
    PostOrder(root->right);
    printf("%d ", root->data);
}

// Number of nodes in the binary tree
int BTSize(BTNode* root)
{
    if (root == NULL)
    {
        return 0;
    }
    return BTSize(root->left) + BTSize(root->right) + 1;
}

// Number of leaf nodes in the binary tree (leaf node: degree 0 node)
int BTLeafSize(BTNode* root)
{
    if (root == NULL)
    {
        return 0;
    }
    if (root->left == NULL && root->right == NULL)
    {
        return 1;
    }
    return BTLeafSize(root->left) + BTLeafSize(root->right);
}

// Number of nodes at the k-th level of the binary tree
int BTLevelKSize(BTNode* root, int k)
{
    if (root == NULL)
    {
        return 0;
    }
    if (k == 1)
    {
        return 1;
    }
    return BTLevelKSize(root->left, k - 1) + BTLevelKSize(root->right, k - 1);
}

// Depth/height of the binary tree
int BTDepth(BTNode* root)
{
    if (root == NULL)
    {
        return 0;
    }
    // Return the deeper of the left or right subtree
    return BTDepth(root->left) > BTDepth(root->right) ? BTDepth(root->left) + 1 : BTDepth(root->right) + 1;
}

// Find the node with value x in the binary tree
BTNode* BTFind(BTNode* root, DataType x)
{
    if (root == NULL)
    {
        return NULL;
    }
    if (root->data == x)
    {
        return root;
    }
    BTNode* leftFind = BTFind(root->left, x); // Search in the left subtree
    if (leftFind)
    {
        return leftFind; // Found in the left subtree, return it
    }
    BTNode* rightFind = BTFind(root->right, x); // Search in the right subtree
    if (rightFind)
    {
        return rightFind; // Found in the right subtree, return it
    }
    return NULL;
}

// Destroy the binary tree
// Post-order traversal for destruction: destroy left subtree, then right subtree, finally the root node
void BTDestroy(BTNode** root)
{
    if (*root == NULL)
    {
        return;
    }
    BTDestroy(&((*root)->left));
    BTDestroy(&((*root)->right));
    free(*root);
    *root = NULL;
}

// Level-order traversal using a queue
void LevelOrder(BTNode* root)
{
    QU q; // Create a queue
    QueueInit(&q);
    QueuePush(&q, root); // Enqueue the root node
    while (!QueueEmpty(&q)) // While the queue is not empty
    {
        // Get the front of the queue and print it
        BTNode* Qhead = QueueFront(&q);
        printf("%d ", Qhead->data);
        QueuePop(&q); // Dequeue the front node
        // Enqueue the left child of the front node
        if (Qhead->left)
        {
            QueuePush(&q, Qhead->left);
        }
        // Enqueue the right child of the front node
        if (Qhead->right)
        {
            QueuePush(&q, Qhead->right);
        }
    }
    QueueInit(&q);
    QueueDestroy(&q);
}

// Check if the binary tree is a complete binary tree using a queue
bool BTComplete(BTNode* root)
{
    QU q; // Create a queue
    QueueInit(&q);
    QueuePush(&q, root); // Enqueue the root node
    while (!QueueEmpty(&q)) // While the queue is not empty
    {
        // Dequeue the front node
        BTNode* Qhead = QueueFront(&q);
        QueuePop(&q);
        if (Qhead == NULL)
        {
            break;
        }
        // Enqueue both the left and right children
        QueuePush(&q, Qhead->left);
        QueuePush(&q, Qhead->right);
    }
    // When empty nodes are encountered, we exit the loop; the queue may not be empty at this point
    while (!QueueEmpty(&q)) // While the queue is not empty
    {
        // Dequeue and check the node
        BTNode* Qhead = QueueFront(&q);
        QueuePop(&q);
        if (Qhead != NULL)
        {
            return false; // If a non-null node is found, the tree is not a complete binary tree
        }
    }
    QueueDestroy(&q);
    return true; // It is a complete binary tree
}

main.c
Testing

#define _CRT_SECURE_NO_WARNINGS
#include"Tree.h"

BTNode* buyNode(DataType x)
{
    BTNode* newnode = (BTNode*)malloc(sizeof(BTNode));
    if (newnode == NULL)
    {
        perror("malloc fail!");
        exit(1);
    }
    newnode->data = x;
    newnode->left = newnode->right = NULL;
    return newnode;
}

BTNode* CreateTree()
{
    BTNode* n1 = buyNode(1);
    BTNode* n2 = buyNode(2);
    BTNode* n3 = buyNode(3);
    BTNode* n4 = buyNode(4);
    BTNode* n5 = buyNode(5);
    BTNode* n6 = buyNode(6);
    n1->left = n2;
    n1->right = n4;
    n2->left = n3;
    n4->left = n5;
    n4->right = n6;
    return n1;
}

void Test()
{
    BTNode* n1 = CreateTree();
    printf("\nPre-order traversal: ");
    PreOrder(n1);
    printf("\nIn-order traversal: ");
    InOrder(n1);
    printf("\nPost-order traversal: ");
    PostOrder(n1);
    // Print node count
    printf("\nsize = %d\n", BTSize(n1));
    // Print number of leaf nodes
    printf("leaf_size = %d\n", BTLeafSize(n1));
    int k = 2;
    printf("Number of nodes at level %d: %d\n", k, BTLevelKSize(n1, k));
    printf("Depth: %d\n", BTDepth(n1));
    // Find node with value 4
    BTNode* find = BTFind(n1, 4);
    printf("%s\n", find == NULL ? "Not found" : "Found!");
    printf("\nLevel-order traversal: ");
    LevelOrder(n1);
    bool ret = BTComplete(n1);
    printf("\n%s\n", ret == false ? "Not a complete binary tree" : "It is a complete binary tree!");
    BTDestroy(&n1);
}

int main()
{
    Test();
    return 0;
}

4. Summary
In this article, we thoroughly explored the linked structure of binary trees and its implementation in C. We began by understanding the basic structure of binary trees and the advantages of dynamic sizing. Then, we introduced various traversal methods, including pre-order, in-order, post-order, and level-order traversals, along with related node counting functions. Next, the article detailed how to check if a binary tree is a complete binary tree, providing the corresponding destruction function for the tree. Finally, through practical examples, we tested these operations, showcasing the importance and flexibility of binary trees in data processing. This article provides readers with a comprehensive understanding and practical code implementation.

💰 Support Us